Võrdus, samasus, võrrand

Võrrandite lahendamisega puutume alateadlikult kokku iga päev. Näiteks poe leti juures arvutades mitu kg banaane või õunu 2 euro eest saab, majapidamises kommunaalteenuste eest makstes ja isegi reede õhtuti mõnelt lõbusalt olemiselt koju tulles. Vaatame selleks ühte ülesannet.

Võrrandite edukaks koostamiseks ja lahendamiseks peame esmalt tutvuma mõningate võrranditega seotud mõistetega.

Võrdused

Kui kaks avaldist ühendatakse võrdusmärgiga, saadakse võrdus.

Näited võrdustest:

DEF: Võrdust, mis on tõene muutujate kõigi lubatavate väärtuste korral,
nimetatakse samasuseks. Ka tõene arvvõrdus on samasus.

Näited:

$1+2=3$
$(a+1)^2=a^2+2a+1$
$\frac{s^2-16}{s(s+4)}=\frac{s-4}{s}$ , kui $s\neq 0$ ja $s\neq -4$

Võrrandid

DEF: Võrrandiks nimetatakse muutujaid sisaldavat võrdust, milles üks või mitu muutujat loetakse otsitavaks ehk tundmatuks.

Võrrandi tundmatuid tähistatakse tavaliselt ladina tähestiku viimaste tähtedega (x,y,z või ka s,t,u,v jne)

DEF: Võrrandi lahenditeks nimetatakse tundmatu(te) selliseid väärtusi, mille asendamisel võrrandisse saame tõese arvvõrduse ehk samasuse.

Kui võrrandi lahendiks sobib tundmatu iga lubav väärtus, siis on see võrrand ühtlasi ka samasus. Sellisel võrrandil on tavaliselt lõpmata palju lahendeid. Näiteks võrrand $x^2 -1=(x-1)(x+1)=2$ on samasus, võrrand $x^2=1$ ei ole samasus.

Kui võrrandil leidub lahendeid, siis öeldakse ka, et võrrand
on lahenduv. Kui võrrandil lahendid puuduvad, siis on võrrand
mittelahenduv.

Näide:

$\frac{3}{x-1}=0$ on mittelahenduv, sestnulli saamiseks peaks olema lugeja null, aga antud juhul on see 3.

Võrdus jaguneb arvvõrdusteks ja võrranditeks.

Arvvõrdus on kas väär või tõene.

Võrraneid saab jagad veel omakorda järgmiselt tõeväärtuse järgi

Võrrand on tõene muutujate kõigi lubatavate väärtuste korral.
Tõene muutujate mõnede väärtuste korral.
Väär muutujate kõigi väärtuste korral.

Ühe tundmatuga võrrandit võib üldkujul esitada avaldiste f(x) ja g(x) võrdusena $f(x) = g(x)$

Võrrandi $f(x) = g(x)$ määramispiirkonnaks nimetatakse tundmatu $x$ nende väärtuste hulka, mille korral nii avaldise $f(x)$ kui ka avaldise $g(x)$ väärtus on määratud (ehk arvutatav).

Tähistuse $f(x)$ võttis kasutusele Leonhard Euler 1734. a. Tähistust $f(x)$ peab võtma kui ühte tervikut. See ei ole $f\cdot(x)$ või mõni muu tõlgendus. Tegu on ühe tervikliku ühendiga, millel ei saa sulge avad või taandada. Täht f määrab ära seosed, mis avaldises kasutatakse ja tähistus (x) muutujad, mis selles avaldises on esitatud.

Määramispiirkonda illustreerib järgnev f-masina skeem: Masinale on antud ette võrrand $\frac{x+1}{x}$ ja see kontrollib määramispiirkonda, asendades masinasse tulevad väärtused võrrandisse ja visates need minema, mis ei sobi.

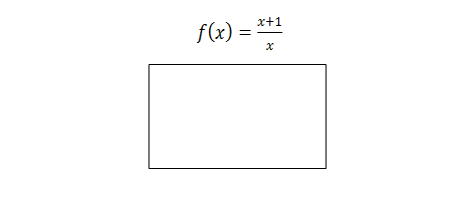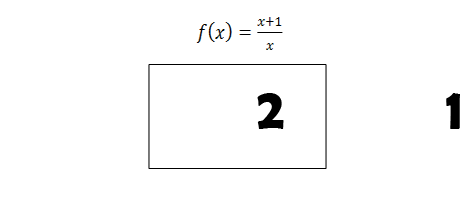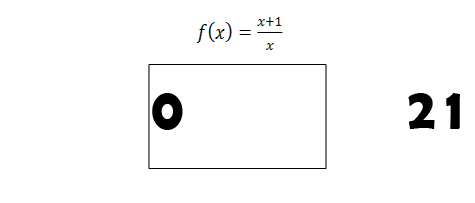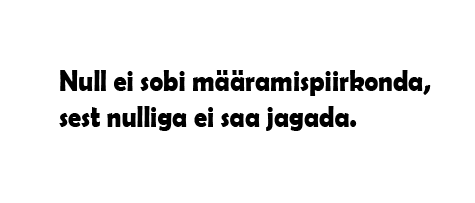
Näiteks võrrandi $\frac{x+1}{x}=2x$ määramispiirkond ei kuulu arv 0 ,sest avaldisel $\frac{x+1}{x}$ puudub väärtus, kui $x=0$ . Kõik ülejäänud reaalarvud kuuluvad selle võrrandi määramispiirkonda.