Õuna ruumala

08/11/201015/03/2011Kaido 4 kommentaari

Palju on kirjutatud artikleid sellest, kuidas matemaatikat tuleks siduda ikka rohkem ja rohkem eluga. Ise olen kohanud palju Pythagorase teoreemi rakendusi torni pikkuse ja maja räästaga seotud ülesannetes. Tuletist olen ka näinud õlilaigu kasvamise ülesandes ja erinevate hetkkiiruste arvutamisel. Mulle ei meenus siiski ühtegi ülesannet integraali elulisest rakendatavusest. Muidugi saame tuletada koonuse ruumala ja kera ruumala arvutamise valemid ning rääkida, et neid saab elus kasutada. Samuti võime rääkida idealiseeritud maalapist, mida ühelt poolt ümbritseb parabool ja teiselt poolt sirge, kuid need ülesanded mõjuvad ikkagi kuidagi kunstlikult. Tegelikult ei ole ju looduses jooned nii ideaalsed. Otsustasin hakata otsima seda ülesannet, et kuidas ikkagi näidata integraali rakendamist elulistes ülesannetes ja poes õuna ostes torkas pähe, et äkki prooviks integraaliga selle ruumala arvutada :D. Naljakas mõte, aga õuna telglõige sarnaneb tegelikult ühe matemaatilise joonega, mida nimetatakse kardioidiks.

Kardioidi ehk südamejoont tekitab fikseeritud ringjoone ümber veereva ringjoone punkt. Kardioid on tegelikult üks joon epitükloidide perekonnast. Kardioid tekib siis, kui pöörleva ja fikseeritud ringjoone raadiuste suhe on 1.

Idee sündis mõttest, et silinder tekib, kui ristkülik pöörleb ümber oma ühe külje. Samuti tekib õuna ruumala, kui kardioid pöörleb ümber oma sümmeetria telje. Küsimuseks jäi, kuidas leida tekkinud ruumala? Enne matemaatilist katsetamist kasutasin vana head Archimedese meetodit. Jätka lugemist →

Picki teoreem

19/10/201024/10/2010Kaido Lisa kommentaar

Kui matemaatikas saab üldse rääkida mingisugusest avastusõppest, siis on Picki valemi tuletamine selle üks paremaid näiteid. Teoreem on nime saanud Austria matemaatiku Georg Alexander Picki (1859 – 1942) järgi. Kui vaadata tema surma aastat, siis see langeb täpselt II maailmasõja keskpaigale. Seos sõjaga on täitsa olemas. Pick suri Tšehhis asuva Theresienstadti koonduslaagris. See koonduslaager oli algupäraselt mõeldud tsehhi juutidele, aga lõpuks laiendati seda kõikidele sõjavangidele.

Pick ongi kõige paremini tuntud oma teoreemiga, mis aitab arvutada hulknurga pindala tema sisepunktide ja küljel asuvate punktide kaudu. Sõnastame nüüd natuke formaalsemalt selle.

Picki teoreem

Kui hulknurga kõik tipud paiknevad täisarvulistes punktides, siis selle hulknurga pindala A avaldub kujul

$A=I+\frac{1}{2}B-1 ,$

kus I ja B on vastavalt vaadeldava hulknurga sees ja seda piirava hulkkülikul olevate täisarvuliste punktide arvud.

Vaatame veel näiteks ühte joonist

Siin on B ( ingl. k Border – raam) = 6 ja I (ingl. k. Interior – sisemus) = 17. Picki valemist saame selle pindalaks A ( ingl. k. Area – pindala)

$A=17+\frac{1}{2}\cdot 6-1= 17+3-1=19$

Tuletamisest pikemalt mõni teine kord

Viited: http://en.wikipedia.org/wiki/Georg_Alexander_Pick, http://mathworld.wolfram.com/PicksTheorem.html, http://www.cut-the-knot.org/ctk/Pick.shtml#applet

Meta: Georg Alexander Pick, Picki teoreem, hulknurk, hulknurga tipud, hulknurga pindala, Geoplaan, sisepunktid, hulkkülik, koonduslaager, II maailmasõda

Kolmnurga sisenurkade summa

14/10/201027/10/2011Kaido Lisa kommentaar

Tabasin ennast täna mõtisklemast, et kas ma olen näinud mingisugust tõestust, et kolmnurga sisenurkade summa on $180^\circ$ . Ise tõestasin selle natuke teisel moel, aga see ka sobib samuti.

Tõestada, et kolmnurga sisenurkade summa on $180^\circ$

Joonestame sirge a läbi punktide A ja B. Joonistame sirge b läbi punkti C nii, et see oleks paralleelne sirgega a. Seda võib teha kasutades ära rombi omadusi.Kuna $a \parallel b$ , siis on $\angle BAC = \angle B'AC$ (paralleelsete sirgete lõikamisel kolmandaga tekkinud paar võrdseid põiknurki (alternate interior angles)) . Lisaks on samal põhjusel $\angle ABC = \angle BCA'$ . Nüüd on juba ilmne, et

$\angle BAC + \angle ABC + \angle BCA = 180^\circ \clubsuit$

See sobib, kuigi ise mõtlesin, et äkki tõestati see algupäraselt läbi ringjoone, sest täispööre on $360^\circ$ . Kui sinna sisse konstrueerida kolmnurk, on iga tipp piirdenurgaks, mille suurus on pool kaare suurusest. Kuna kaarte summa on $360^\circ$ , siis kolmnurga nurkade summa peab olema $180^\circ$ . Aga vähemalt on selge, miks see nii on.

Kasutatud materjalid

http://www.apronus.com/geometry/triangle.htm

Meta: Kolmnurkade sisenurkade summa, sada kaheksakümmend kraadi, täisnurkne kolmnurk, kolmnurk, põiknurk, paralleelne sirge, romb

Thales [Miletus, 624-546 BC]

14/07/201003/10/2010Kaido Lisa kommentaar

Proovige kujutada ette Kreeka tsivilisatsiooni 600 e.kr. Kujutage ennast õitsvasse ärilinna. Kreeklastel oli paljude ümbritsevate rahvastega väga intensiivne kaubandus. Sellepärast olid paljud Kreeka linnad rikkad ja sellega kaasnes kunst, teadus ning filosoofia. Siiski oli ka probleeme.

Poliitlist kliimat mõjutas orjandus ja suurkaupmehed. Linnasid juhtisid sageli hoolimatud türannid – aristokraadid ja ülirikkad kaupmehed. Umbes aasta 585 e.kr elas Miletuses mees, kelle nimi oli Thales. Ta oli üks seitsmest Kreeka targast

Thales oli käinud Egiptuses geomeetriat õppimas. Ta suutis kuidagi anda Egiptuse meetoditele uue lähenemise, sest tagasi tulles hämmastas ta paljusid oma erakordsete matemaatiliste võimetega. Thales arvutas laevade kauguse merel maalt võetud kahe vaatluspunkti alusel ja ta teadis, kuidas arvutada püramiidi kõrgust tuginedes selle varjule. Kuulsaks sai ta 585 e. kr toimunud päikesevarjutuse ennustamisega.

Hoolimata oma tarkusest oli Thales vaene mees. Miletuse elanikud mõnitasid teda sellepärast, et mis kasu on filosoofiast ja tarkusest, kui ta ei jaksa üüri maksta. Tema aeg siiski saabus. Õigel ajal tarkust näidates kogus Thales varsti üpris kena varanduse.

Thales oli rohkem matemaatik kui filosoof, kuigi antikkajal neil eriti vahet ei olnud.

Meile on Thales kõige paremini tuntud oma kuulsa teoreemiga:

Ringjoone diameetrile toetuv piirdenurk on täisnurk.

TÕESTUS

Olgu M läbi punktide A, B ja C joonestatud ringjoone keskpunkt. Siis r=AM=MB=MC.

Seega on $\triangle AMC$ ja $\triangle CMB$ võrdhaarsed.

Kui tähistame $\angle BMC=:\alpha$ , siis vastavalt võrdhaarse kolmnurga omadusele, $\angle MCB=90^\circ-\frac{\alpha}{2}$ ja $\angle CMA=180^\circ-\alpha$ . Seega $\angle ACM=\frac{\alpha}{2}$ .

Liites vastavad nurgad saame, et

$\displaystyle \angle ACB=\angle MCB+\angle ACM=90^\circ-\frac{\alpha}{2} + \frac{\alpha}{2}=90^\circ \clubsuit$

See on geomeetriline tõestus. Analüütilises geomeetrias on seda võimalik teha kasutades näiteks ringjoone võrrandit ja avaldada Pythagorase teoreemist tingimuse täisnurkse kolmnurga olemasoluks.

Kuigi see paistis lihtsa vaatluse tulemus, oli Thales esimene, kes selle sõnastas ja pani aluse deduktiivsele teadusele. See on protsess, kus mitme vaatluse tulemusena järeldatakse midagi täpsemat ehk üldiselt minnakse üksikumale.

Selle väikese jutustuse Thalesest lõpetame tema enda tsitaadiga: “Igas objektis on natuke jumalust!”

http://www.thebigview.com/greeks/thales.html

http://myyn.org/m/article/proof-of-thales-theorem/

Meta: Thales, Thalese teoreem, täisnurkne kolmnurk, ringjoone diameeter, Miletus, deduktsioon, deduktiivne lähenemine, täisnurk, põhikool, III kooliaste, matemaatika.

Projekteerimisest

09/04/201003/10/2010Kaido Lisa kommentaar

Enne ühe tõestuse esitamist siin oleks vaja selgitada, mis üldse on projekteerimine ja projektsioon. Matemaatika sõnastikus on loetletud päris palju termineid. Osad geomeetria jaoks ja osad funktsioonide jaoks, sest funktsioonid ja kujutused on samuti mingis mõttes projekteerimised. Aga nüüd täpsemalt. Leidsin TTÜ õpijuhendi, mis pilti natuke selgemaks tegi.

Projekteerimine jaotub laias laastus tsentraalprojekteerimiseks ja paralleelprojekteerimiseks.

TSENTRAALPROJEKTEERIMINE (central projection) – Projekteerivad kiired lähtuvad kõik ühest punktist, mida
nimetatakse silmapunktiks. Tulemiks on tsentraalprojektsioon ehk perspektiiv

PARALLEELPROJEKTEERIMINE (parallel projection) – Kujutamiskiired on omavahel paralleelsed (silmapunkt
lõpmata kaugel). Tulemiks on paralleelprojektsioon.

Meid huvitab lihtsam variant ehk paralleelprojekteerimine. Paralleelprojekteerimine jaotub veel omakorda kaldprojekterrimiseks (oblique projection) ja ristprojekteerimiseks (orthogonal projection).

Nüüd on enamvähem selge, mis kastis me tegutsema hakkame. Vaatamegi siis lähemalt ristprojekteerimist.

Nii mulle kui paljudele teistele õpetati kolmnurka ja tema projektsioone alati selle lihtsustatud variandi abil. Ega tegelikult ei seletatudki eriti ära, kuidas need projektsioonid sinna alusele tulevad. Lihtsalt tõmba tipust kõrgus ja jupp, mis jääb külje a poole on a projektsioon (roheline) ja b poole on külje b projektsioon (kollane). Siinkohal on tegu just ristprojektsiooniga. Projektsioon ei teki sinna küljele c kuskilt lambist. Need saadakse sinna ristlõikude abil. Koolis ja siin joonisel on põhimõtteliselt projekteeritud ainult üks punkt. Selleks on kolmnurga tipp. Terve b projektsiooni saamiseks peaksime tõmbama ristlõigud igast külje b punktist. Kuna neid on hästi palju, kuid siiski lõplik hulk, eeldatakse vaikimisi, et see protsess on tehtudja märgitakse ainult siis projektsiooni algus- ning lõpp-punkt. Sama asi küljega a. Tänu antud kolmnurga omadusele osutub viimane ristlõik kolmnurga kõrguseks.

Kõik on ilus, kui kolmnurk on teravnurkne. Mis juhtub aga siis, kui see on nürinurkne ?

Siin juhtub selline asi, et kui ei ole tegu kõige pikema küljega, on vaja projekteeritavale küljele teha pikendus ja projekteerimine käib pikenduse peale. Nagu näha, läheb siin kolmnurga kõrgus kolmnurgast välja. Ei maksa muretseda. kõik asjad jäävad siiski kehtima ja tõesti — kõrgus võib olla kolmnurgast väljas. Projektsioonidega juhtub see asi, et üks muutub teise osaks. Antud juhul on siis projekteeritud küljed a ja b küljele c.

Siin siis näide sellest, millised näevad välja külje a (roheline) ja c ( kollane) projektsioonid küljele b. Edasi võib igaüks ise mõelda, millised näevad välja näiteks selle sama viimase kolmnurga ristprojektsioonid küljele a.

Kokkuvõtteks:

Ristprojektsiooni tegemiseks määrame ära kõigepealt baaskülje, millele hakkame projekteerima. Projektsiooni saamiseks tõmbame projekteeritava külje igast punktist ristlõigud baasküljele, kuni kõik punktid on projekteeritud ( lihtsuse mõttes võib tõmmata ainult algus ja lõpp-punktist need ristlõigud). Olenevalt baasküljest võivad nürinurkse kolmnurga puhul projektsioonid kattuda. Samuti võib vaja minna külje pikendusi ning mõni ristlõikudest võib minna kolmnurgast välja. See ei ole anomaalia või müstika vaid lihtsalt üks nürinurkse kolmnurga omadusi.

Kasutatud materjal:

http://www.e-uni.ee/konverents/2004/stend/Projekteerimine.pdf

——————————————————————————————-

Meta: projektsioon, tsentraalprojektsioon, paralleelprojektsioon, kaldprojektsioon, ristprojektsioon, projekteerimine, nürinurkne kolmnurk, teravnurkne kolmnurk, kõrgus, ristlõik

Euleri valem täisnurkse kolmnurga puhul

01/04/201003/10/2010Kaido 5 kommentaari

Netist seda valemit nii kergelt ei leia. Euler oli produktiivne mees ja pigem tuntakse tema valemeid rohkem Algebras kui geomeetrias. Ülesanne on tegelikult kergesti arusaadav.

Avaldada täisnurkse kolmnurga siseringjoone ja ümberringjoone keskpunktide vaheline kaugus sise- ja ümberringjoone raadiuste r ja R kaudu.

Kui kellelgi on meelest ära läinud, kuidas neid ringjooni saadi või kus keskpunkt asub, siis mõned meeldetuletused:

Siseringjoone keskpunkt asub nurgapoolitajate lõikepunktis
Ümberringjoone keskpunkt on täisnurkse kolmnurga hüpotenuusi keskpunktiks

Rohkem polegi vist vaja teada. Seega esialgne joonis näeb välja järgnev:

Punane lõik on see, mille pikkust leidma hakkame. Joonist on vaja täiendada natuke. Ümberringjoone keskpunkt asus hüpotennusi keskpunktist. Siit saame konstrueerida sellest punktist lähtuvad kolmnurga kesklõigud. Joonestame ka välja siseringjoone raadiused ja pikendame neist ühte, et see lõikuks hüpotenuusi.

Päris palju toiminguid, mida vaja teha ja peas ette kujutada. Kui ei saanud päris täpselt aru, siis vaadake järgnevat joonist, et mida me pikendasime ja mida me juurde joonistasime.

Nii, ärme unusta eesmärki, milleks oli kaugus kahe ringjoone keskpunkti vahel. Keskpunkt d avaldub selle punase kolmnurga külgede kaudu 8 mille tähistasin vastavalt x ja y. See on tegelikult täisnurkne kolmnurk, sest raadiused on risti vastavate nurga haaradega ja kesklõigud on samuti paralleelsed vastavate alustega. Siit saame, et $d^2=x^2+y^2$ . Nüüd edasi oleks vaja avaldada kuidagi x ja y. Tänu alust a poolitavale kesklõigule ja küljesuurusega r olevale ruudule, avaldub x kujul $x=\frac{a}{2}-r$ . Sabasuguse ideega saame avaldada ka y. Ainult nüüd külje b kaudu. $y=\frac{b}{2}-r$ . Siit:

$d^2=x^2+y^2=(\frac{a}{2}-r)^2+(\frac{b}{2}-r)^2=\frac{a^2}{4}-ar+r^2+\frac{b^2}{4}-br+r^2=\frac{a^2+b^2}{4}+2r^2-ar-br=R^2+2r^2-r(a+b)=R^2+r(2r-a-b)$

Kes vahepeal aru ei saanud, kuidas a-st ja b-st järsku R sai, siis $a^2+b^2=c^2 \Rightarrow c^2=4R^2$ , sest c =2R.

Nüüd pean ma kuskilt foorumisügavustest kaevama üles postituse, kus avaldasime täisnurkse kolmnurga siseringjoone raadiuse külgede kaudu:

Üks väike jutuke täisnurkse kolmnurga siseringjoonest

Sa vahi, kus seda vaja läheb :). Ok, sealt saime valemiks $r=\frac{a+b-c}{2} \Rightarrow 2r=a+b-c$

Nüüd saame oma asja edasi teha: $\ldots R^2+r(2r-a-b)=R^2+r(a+b-c-a-b)= R^2-rc=R^2-2Rr$ ehk lõplikult:

$d(r,R)=R^2-2Rr$

————————————————————————

Meta: Euler, täisnurkne kolmnurk, siseringjoon, ümberringjoon, hüpotenuus, kesklõik, ümberringjoone raadius, siseringjoone raadius, keskpunkt.

Üks väike jutuke täisnurkse kolmnurga siseringjoonest

11/02/201003/10/2010Kaido 2 kommentaari

See ülesanne käib läbi kindlasti paljudest keskkoolidest ja võib võtta vahepeal juhtme kokku.

ÜLESANNE

Avalda täisnurkse kolmnurga (right triangle) siseringjoone raadius täisnurkse kolmnurga külgede a, b ja c kaudu.

Tähistame siis kolmnurga küljed vastavalt tähtedega a, b ja c. Nüüd konstrueerime siseringjoone. Selleks konstrueerime nurgapoolitajad (angle bisector) ja leiame nende lõikepunkti. See ongi siseringjoone keskpunktiks. Edasi joonestame välja raadiused. Need on risti külgedega, sest külgi võib vaadelda ka kui siseringjoone puutujaid ja raadiused on risti puutujatega. Kui oleme raadiused välja joonestanud, avaldame vastavad jupid külgede kaudu. Nüüd vaadake natuke joonist. Miks on hüpotenuusil olev a-r võrdne haaral a oleva a-r´ga. See tuleb tegelikult nurgapoolitja omadusest. Nimelt tekitab see kaks kongruentset kolmnurka ja kongruentsetes kolmnurkades on vastavad küljed võrdsed. Kuidas nüüd c avaldub.

c = b – r + a – r , millest

c = b + a – 2r, millest

2r = a + b – c, millest

$r=\frac {a + b - c}{2}$

Aplaus, oleme avaldanud täisnurkse kolmnurga siseringjoone raadiuse tema külgede kaudu.

Seda saab teha ka tegelikult üldisest valemist. Nimelt kehtib iga suvalise kolmnurga puhul

S = pr , kus p on pool ümbermõõtu ja S on pindala

$r = \frac{S}{p}$

$r= \frac{\frac{ab}{2}}{\frac{a+b+c}{2}}$

$r = \frac{ab}{a+b+c}$

Kehtib samuti. Kes ei usus, pange arvud asemele ja proovige.

—————–

meta: siseringjoon, siseringjoone raadius, täisnurkne kolmnurk, nurgapoolitaja

Eukleidese teoreem

03/02/201021/10/2010Kaido Lisa kommentaar

Andsin esmalt Eukleidese tõestuse Steineri teoreemi kaudu. See tuli küll välja, aga kui hakata ajalooliselt mõtlema, siis Eukleides elas ikka mitu sada aastat varem. Kuidas tema seda tegi ?

Eukleidese teoreem

Täisnurkse kolmnurga kaatet on hüpotenuusi ja hüpotenuusil võetud selle kaateti projektsiooni keskmine võrdeline.

Järelikult peame näitama, et $a^2=cf$ ja $b^2=cg$ , kus f ja g on siis nende kaatetite ristprojektsioonid.

Vaatleme täisnurkset kolmnurka ABC. $\angle DBA = \angle DCB$ , sest mõlemad on $90^\circ - \angle DAB$ . Analoogsel põhjusel on $\angle BAD = \angle CBD$ . Järelikult on kolm sarnast kolmnurka, ehk

$\triangle ABD \sim \triangle BDC \sim\triangle ABC$

Vaatleme esmalt seost $\triangle ABD\sim \triangle ABC$ . Me saame välja kirjutada tänu sarnasusele vastavate külgede suhted

$\frac{b}{c} =\frac{g}{b} \Rightarrow b^2=cg$

Oleme saanud kätte ühe tulemuse Eukleidese teoreemist. Teise suhte saamiseks vaatame sarnasust $\triangle BDC\sim \triangle ABC$

$\frac{a}{c} =\frac{f}{a} \Rightarrow a^2=fg$

Nii, et Eukleidese teoreem tõestatud. Järgnev on siis tõestus Steineri teoreemi kaudu. Kes enam teisest tõestusest ei hooli, siis ilus jätk oleks pöörduda Pythagorase teoreemi tõestuse juurde, sest Eukleides tegi need järeldused just omadest tulemustest.

Alustaks oma kirjutist lausega, mis võib paljusid kooligeomeetrias välja aidata: See mis kehtib iga kolmnurga korral, kehtib kindlasti ka täisnurkse kolmnurga korral. Nii on ka Eukleidese teoreemiga:

Tegu on vahetu järeldusega teoreemis lõikajast ja puutujast, mis väitis :

Kui väljaspool ringjoont võetud punktist on ringjoonele tõmmatud lõikaja ja puutuja, siis puutuja lõik antud punktist puutepunktini on keskmine võrdeline lõikaja osadele, mis on võetud antud punktist lõikepunktideni ringjoonega.

See aga on meil juba tõestatud.

Nüüd oleks sobilik lisada ka millised seosed siis valitsevad tõestatud teoreemide vahel, millised on vahetud järeldused ja erijuhud ning kus saab tõestamisel mõnda eelnevat teoreemi kasutada.

Teoreem täisnurkse kolmnurga kõrgusest

03/02/201003/10/2010Kaido Lisa kommentaar

Teoreem täisnurkse kolmnurga kõrgusest

Täisnurkse kolmnurga kõrgus on hüpotenuusil võetud kaatetite projektsioonide keskmine võrdeline

Antud joonise järgi tähendaks see, et

BC²=DC · AC

Tõestus #1: Olgu kolmnurk DBA täisnurkne. Joonestame läbi punktide DB ringjoone. Kuna AB on joonestatud ringjoone puutuja ja keskpunktist tõmmatud raadius on puutujaga risti ja seega läbib ka kõõl DB keskpunkti, siis vastavalt ringjoone diameetri definitsioonile on kõõl DB ringjoone diameeter.

Tõestus on tegelikult tänu varem tõestatud teoreemile puutujast ja kõõlust lihtne. Et siduda kõrgus kuidagi nende otsitavate suurustega, proovime näidata, et kolmnurgad DCB ja CAB on sarnased. Nad on mõlemad täisnurksed, sest vastavalt Thalese teoreemile on ringjoone diameetrile toetuv piirdenurk täisnurk. Vastavalt teoreemile puutujast ja kõõlust on nurgad ABC ja BDC võrdsed. Seega tunnuse NN põhjal on kolmnurgad DCB ja CAB sarnased. Kirjutame välja vastavate külgede suhted:

BC/DC = CA/BC

väike vihje neile, kellel see kolmnurga pööramine eriti hästi välja ei tule ja kuidagi ei saa aru, millised vastavad küljed on. Vaadake, milliste nurkade vastu või vahele see külg jääb. Näiteks antud joonise põhjal jääb külg BC väiksemas kolmnurgas oranžiga tähistatud nurga vastu, suuremas kolmnurgas on oranži nurga vastas AC. Väiksemas kolmnurgas jääb oranži ja täisnurga vahele külg DC, suures kolmnurgas jääb täisnurga ja oranži nurga vahele BC ja saategi vastavad küljed kätte.

Võrde põhiomadusest saamegi nüüd seosest

BC/DC = CA/BC => BC²=DC · AC

Tõestus #2:

Kellele võib olla see teise teoreemi kaudu tõestamine eriti ei meeldi, siis pakun ka otsese tõestuse välja.

Olgu meil antud täisnurkne kolmnurk ABC ja olgu DC sellele joonestatud kõrgus. Tähistame nurga ACD tähisega β. Siis nurk β = 90°- α . Vaatame kolmnurka ABC, siis nurk CBA avaldub kujul 90°- α = β. Järelikult tunnuse NN põhjal on kolmnurgad ACD ja CDB sarnased. Jääb üle kirjutada välja vastavad suhted:

CD/DB = AD/CD => CD²= AD · DB

Steineri teoreem

02/02/201011/04/2011Kaido Lisa kommentaar

Steineri teoreem, nime saanud Jakob Steineri (1796 – 1863) järgi, on tavaliselt sees paljudes keskkooli geomeetria osa puudutavates õpikutes, kuid harva kannab ta seal oma õiget nime. Selles peatükis räägime kolmest teoreemist:

Teoreem: Lõikajate (secant) nende osade korrutised, mis on võetud lõikajate ühisest punktist lõikepunktideni ringjoonega, on võrdsed.

Seega tahame näidata, et PA · PB = PC · PD

Tõestus: Olgu meil antud ringjoon ja kaks lõikajat ühise punktiga P. Lõigaku nad ringjoont vastavalt punktides A, B, C, D. Tõmbame ringjoonele kõõlud AD ja BC. vastavate suhete kehtivuseks on mõtekas näidata, et vastavad kolmnurgad on sarnased. vaatamegi kolmnurki APD ja PBC. Näeme kohe, et neil on ühine tipp P, seega ka ühine nurk P. Lisaks toetub nurk BAD samale kaarele, mis BCD. Teatavasti on samale kaarele toetuvad piirdenurgad võrdsed. Seega on kolmnurgad APD ja PBC tunnuse NN põhjal sarnased. Kirjutame välja vastavad külgede suhted:

Millest võrde põhiomadust kasutades järeldubki, et PA · PB = PC · PD #

Enne kui läheme Steineri teoreemi ühe erijuhu juurde, kus üks lõikajatest on hoopis ringi puutuja, tõestame ära teoreemi lõikajast ja kõõlust.

Teoreem puutujast ja kõõlust:
Puutepunkti tõmmatud kõõlu ja puutuja vaheline nurk on võrdne sellele kõõlule konstrueeritud piirdenurgaga.

Tõestus: Olgu meil antud ringjoon ning puutuja puutepunktiga C ning asugu punktid A ja B sellel puutujal nagu näidatud kõrvaloleval joonisel. Olgu puutepunkti konstrueeritud kõõl DC ning kõõlule konstrueeritud piirdenurk DEC. Peame näitama, et nurk DCB on võrdne nurgaga DEC.

Joonistame kõõlu FD // AB
Joonestame kiire CO ja olgu punkt G kõõlu FD ja kiire CO lõikepunkt.
FD on risti CG-ga (sest OC on risti puutujaga AB)
Nurk DFC on võrdne nurgaga DEC, sest nad toetuvad samale kaarele
OF = OD (ringi raadius)
Nurk OFG = nurgaga ODG , sest kolmnurk OFD on võrdhaarne
Nurk FGO = nurgaga DGO = täisnurk, sest CG on risti FD-ga.
Vastavalt punktidele 5,6,7 ja tunnuse NKN põhjal on kolmnurgad OFG ja ODG kongruentsed.
FG = GD, punkti 8 põhjal
Nurgad FGC ja DGC on täisnurgad vastavalt punktile 3.
GC =GC
Vastavalt punktidele 9, 10 ja 11 on kolmnurgad FGC ja DGC kongruentsed.
Nurk DFC on võrdne FDC-ga, kui kongruentsete kolmnurkade vastavad nurgad.
Nurk FDC on võrdne nurgaga DCB, kui paar võrdseid sisemisi põiknurkasid (alternate interior angles).
Vastavalt punktidele 4, 13, 14 on nurgad DCB ja DEB võrdsed.

Sellel on olemas tegelikult palju lihtsam tõestus.

Tõestus#2

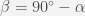Olgu meil antud siis ringjoon keskpunktiga O raadiusega OA ja puutugu sirge s seda ringjoont punktis A. Peame näitama, et $\alpha = \alpha'$ . Teame, et ringjoone raadius on risti puutujaga ( tuleb nurgapoolitja omadusest). Järelikult on $OA \bot s$ . Nurk $\beta$ on avaldatav siis kujul $\beta=90^\circ-\alpha$ . Kuna OA= OB kui ringjoone raadius, siis on kolmnurk OAB võrdhaarne. Järelikult on alusnurgad võrdsed ehk 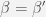$\beta = \beta'$ . Kuidas avaldub siis kolmnurga nurk BOA, mis on ühtlasi selle ringjoone kesknurgaks

$180^\circ - [2(90^\circ-\alpha)]= 180^\circ - 180^\circ + 2\alpha=2\alpha$

Kuna piirdenurk on pool kesknurgast, siis järelikult ongi $\alpha = \alpha' \clubsuit$

Läheme nüüd Steineri teoreemi erijuhu juurde.

Teoreem lõikajast ja puutujast: Kui väljaspool ringjoont võetud punktist on ringjoonele tõmmatud lõikaja ja puutuja, siis puutuja lõik antud punktist puutepunktini on keskmine võrdeline lõikaja osadele, mis on võetud antud punktist lõikepunktideni ringjoonega.

Tõestus: Olgu meil antud ringjoon, lõikaja ACD ja puutuja AB. Peame näitama, et

AB²=AC · AD

Nurk CAB on võrdne nurgaga BAD (sama nurk)
Nurk CBA on võrdne nurgaga BDA vastavalt eelnevalt tõestatud teoreemile puutujast ja kõõlust
Järelikult on tunnuse NN põhjal kolmnurk ACB sarnane kolmnurgaga ADB
Siit saame kolmnurkade sarnasuse põhjal, et AB: AD = AC: AB, millest AB²=AC · AD

Materjale

Pealkiri: Circles, Tangent-Chord Theorem, Intersecting Chord Theorem and Tangent-secant Theorem
Alapealkiri: –
Autor: –
Faili tüüp: pdf
Maht: 8lk

———————————————————————————————
Meta: Ringjoon, raadius, diameeter, kõõl, kesknurk, postulaat, järeldus, puutuja, teoreem puutujast ja kõõlust, lõikaja, piirdenurk

Pealkiri: Nurgad, ringid, hulknurgad
Alapealkiri: –
Autor: –
Faili tüüp: pdf
Maht: 6 lk

———————————————————————————————-
Meta: ülesanded, kesknurk, piirdenurk, teoreem lõikuvatest kõõludest, teoreem lõikajalõikudest e. Steineri teoreem, teoreem puutujalõigust ja lõikajalõikudest,

Kasutatud materjalid:

http://jwilson.coe.uga.edu/EMT669/Student.Folders/Jones.June/steiner/steinerthm.html

NUMBRID

Matemaatikaalane blogi

XI Integraal. Planimeetria kordamine

Õuna ruumala

Picki teoreem

Kolmnurga sisenurkade summa

Thales [Miletus, 624-546 BC]

Projekteerimisest

Euleri valem täisnurkse kolmnurga puhul

Üks väike jutuke täisnurkse kolmnurga siseringjoonest

Üks väike jutuke täisnurkse kolmnurga siseringjoonest

Eukleidese teoreem

Teoreem täisnurkse kolmnurga kõrgusest

Steineri teoreem

Jaga seda :

Jaga seda :

Jaga seda :

Jaga seda :

Jaga seda :

Jaga seda :

Jaga seda :

Jaga seda :

Jaga seda :

Jaga seda :